Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 67°. Ответ дайте в градусах.
Источник: ОГЭ Ященко 2024 (36 вар)
Решение:
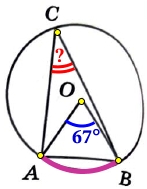
Величина вписанного угла (∠АСВ) в два раза меньше центрального (∠АОВ), опирающегося на ту же дугу (‿АВ):
\angle ACB=\frac{\angle AOB}{2}=\frac{67^{\circ} }{2}=33,5^{\circ}
Ответ: 33,5.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 18
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.
