Четырёхугольник АВСD вписан в окружность. Прямые АВ и СD пересекаются в точке К, ВК = 8, DК = 24, ВС = 18. Найдите АD.
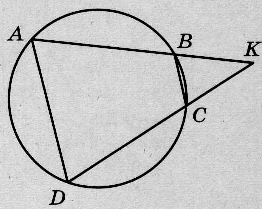
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
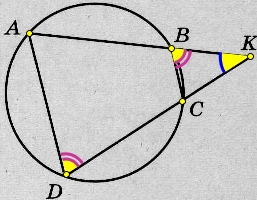
В ΔКАD и ΔКBC ∠К общий.
Четырёхугольник АВСD вписан в окружность сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180º
∠ADC = 180º – ∠ABC
∠ABC и ∠CBK смежные их сумма равна 180º:
∠ABC + ∠CBK = 180º
∠CBK = 180º – ∠ABC
Из этих двух равенств получаем:
∠ADC = ∠CBK
Тогда ΔКАD и ΔКBC подобны по двум равным углам. Их соответствующие стороны пропорциональны, составим пропорцию:
\frac{AK}{CK}=\frac{DK}{BK}=\frac{AD}{BC}\\\frac{DK}{BK}=\frac{AD}{BC}\\\frac{24}{8}=\frac{AD}{18}\\\frac{3}{1}=\frac{AD}{18}\\3\cdot 18=1\cdot AD\\AD=3\cdot 18=54
Ответ: 54.