Центральный угол опирается на хорду АВ длиной 10. При этом угол АОВ равен 60° (см. рис. 18). Найдите радиус окружности.
Источник: ОГЭ Лысенко 2022 (40 вар)
Решение:
Способ №1
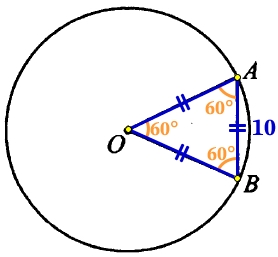
ОA = ОВ – как радиусы окружности, значит ΔАОВ равнобедренный, углы при основании равны, зная, что ∠АОВ = 60°, найдём чему равны оставшиеся два угла треугольника (сумма углов любого треугольника равна 180°):
∠A=∠B=\frac{180°–∠AOB}{2}=\frac{180°–60°}{2}=\frac{120°}{2}=\color{DarkOrange} 60°
Все углы в треугольнике равны 60°, значит ΔАOB равносторонний, все стороны в нём равны:
AB = OA = OB = 10
Т.к. ОА и ОB это радиусы, значит r = 10.
Ответ: 10.
Решение:
Способ №2
ΔАОВ равнобедренный, т.к. боковые стороны являются радиусами окружности и равны ОА = ОВ.
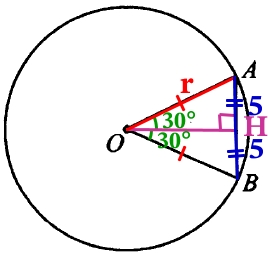
Проведём высоту ОН, которая будет являться медианой и биссектрисой:
∠АОН = ∠ВОН = ∠АОВ/2 = 60°/2 = 30°
АН = НВ = АВ/2 = 10/2 = 5
В прямоугольном ΔАОН через синус ∠АОН найдём радиус ОА.
Синус острого угла прямоугольного треугольника – это отношение противолежащего катета к гипотенузе:
sin\angle AOH=\frac{AH}{OA} \\sin\, 30^{\circ}=\frac{5}{r}\\\frac{1}{2}=\frac{5}{r}\\r=2\cdot 5=10
Ответ: 10.