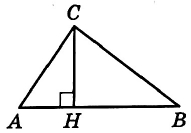
На гипотенузу АВ прямоугольного треугольника ABC опущена высота СН, АН = 7, ВН = 28. Найдите СН.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
ΔАBC и ΔACH подобны по двум равным углам (∠A – общий, ∠ACB = ∠AHC = 90°).
Точно так же подобны ΔАВС и ΔCBH (∠B – общий и ∠ACB = ∠BHC = 90°), поэтому ∠A = ∠BCH.
Наконец, ΔACH и ΔCBH также подобны по двум равным углам (в этих треугольника углы с вершиной H прямые и ∠A = ∠BCH). В подобных треугольниках, соответствующие стороны пропорциональны:
\frac{AH}{CH}=\frac{CH}{BH}\\\frac{7}{CH}=\frac{CH}{28}\\CH\cdot CH=7\cdot 28\\CH^{2}=196\\CH=\sqrt{196}=14
Ответ: 14.