Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно, АС = 36‚ МN = 28. Площадь треугольника АВС равна 162. Найдите площадь треугольника MBN.
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
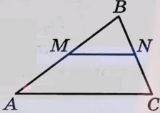
ΔАВС и ΔMNB подобны по двум равным углам (∠В общий, ∠ВАС = ∠ВМN – как соответственные при параллельных прямых и секущей).
Найдём коэффициент подобия треугольников:
k=\frac{AC}{MN}=\frac{36}{28}=\frac{9}{7}
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия:
\frac{S_{\Delta ABC}}{S_{\Delta MBN}}=k^{2}\\ \frac{162}{S_{\Delta MBN}}=(\frac{9}{7})^{2}\\\frac{162}{S_{\Delta MBN}}=\frac{81}{49}\\S_{\Delta MBN}=\frac{162\cdot 49}{81}=2\cdot 49=98
Ответ: 98.