В параллелограмме АВСD отмечена точка М – середина стороны ВС. Отрезки ВD и АМ пересекаются в точке К. Найдите длину отрезка ВК, если ВD = 15.
Источник: Ященко ЕГЭ 2022 (30 вар).
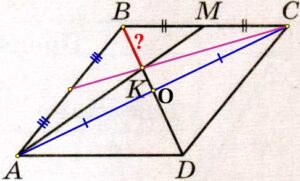
Решение:
Проведём диагональ АС параллелограмма:
В получившемся ΔАВС АМ – медиана (М – середина стороны ВС), ВО – медиана (диагонали параллелограмма в точке пересечения делятся пополам).
Найдём ВО:
ВО = BD/2 = 15/2 = 7,5
По свойству медиан треугольника, все три (третью нарисовал для наглядности) медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Получаем, что ВО делится на 2 + 1 = 3 части, и 2 части из них это отрезок ВК. Одна часть равна:
ВО/3 = 7,5/3 = 2,5
2 части или ВК равен:
2·2,5 = 5
Ответ: 5.