Решение №2388 Найдите точку максимума функции у=(х-5)^2∙е^(х-7).

Решение:

y = (x − 5)²∙e^x−7

    Найдём производную функцию:

𝑦′ = ((𝑥−5)²)′∙𝑒^𝑥−7 + (𝑥−5)²∙(𝑒^𝑥−7)′ = 2·(𝑥−5)∙𝑒^𝑥−7 + (𝑥−5)²∙𝑒^𝑥−7 = 𝑒^𝑥−7(2·(𝑥−5) + (𝑥−5)²) = 𝑒^𝑥−7(2x – 10 + x² – 10x + 25) = 𝑒^𝑥−7(x² – 8x + 15)

    Найдём нули функции:

𝑒^𝑥−7(x² – 8x + 15) = 0
𝑒^𝑥−7 = 0 корней нет
или
x² – 8x + 15 = 0
D = (–8)² – 4·1·15 = 4 = 2²

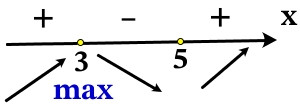
    Определим знаки производной функции и изобразим поведение функции:

    Точка максимума х = 3.

Ответ: 3.