Решение:
Из формулы объёма шара найдём радиус:
V_{шар}=\frac{4}{3}\pi R^{3}=12\pi\\\frac{4}{3}\pi R^{3}=12\pi\\\frac{4}{3} R^{3}=12\\R^{3}=\frac{12}{\frac{4}{3}}=\frac{12\cdot 3}{4}=9\\R=\sqrt[3]{9}
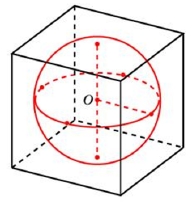
По рисунку видим, что сторона куба равна 2 радиусам:
a=2\cdot \sqrt[3]{9}
Объём куба:
V_{куб}=a^{3}=(2\cdot \sqrt[3]{9})^{3}=2^{3}\cdot 9=8\cdot 9=72
Ответ: 72.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.