Найдите тупой угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 42°. Ответ дайте в градусах.
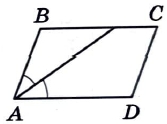
Источник: ОГЭ Ященко 2024 (36 вар)
Решение:
Биссектриса делит угол пополам:
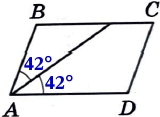
Тогда весь ∠А равен:
∠А = 42° + 42° = 84°
Это острый угол параллелограмма (угол меньше 90° – острый).
Углы ∠А и ∠В односторонние (при AD||BC и секущей АВ) их сумма равна 180°. Найдём тупой ∠В:
∠В = 180° – ∠А = 180° – 84° = 96°
Ответ: 96°.