Диагонали АС и ВD трапеции АВСD с основаниями ВС и АD пересекаются в точке О, ВС = 4, АD = 9, АС = 26. Найдите АО.
Источник: ОГЭ Ященко 2022 (36 вар)
Решение:
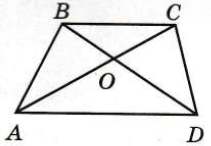
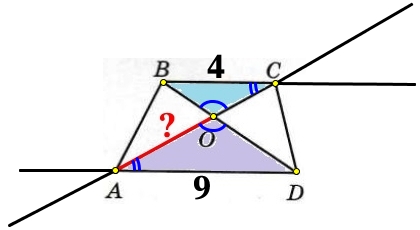
ΔВОС подобен ΔAOD по двум равным углам: ∠ВОС = ∠АОD как вертикальные, ∠ОСВ = ∠ОАD как накрест лежащие при параллельных прямых ВС и АD, и секущей АС.
Соответствующие стороны пропорциональны, запишем отношение:
\frac{АО}{ОС}=\frac{AD}{BC}\\\frac{АО}{ОС}=\frac{9}{4}
Выразим ОС через АС и АО:
ОС = АС – АО = 26 – АО
Подставим:
\frac{АО}{26-АО}=\frac{9}{4}
4·АО = 9·(26 – АО)
4·АО = 9·26 – 9·АО
4АО = 234 – 9АО
4АО + 9АО = 234
13АО = 234
АО = 234/13 = 18
Ответ: 18.