а) Решите уравнение sinx·cos2x – √3cos2x + sinx = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку [\frac{5\pi}{2};4\pi].
Источник: Ященко ЕГЭ 2024 (36 вар)
Решение:

б) С помощью числовой окружности отберём корни принадлежащие отрезку [\frac{5\pi}{2};4\pi]:
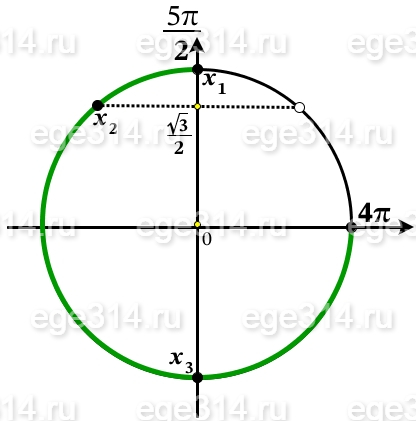
x_{1} = \frac{5\pi}{2}\\x_{2}=2\pi+\frac{2\pi}{3}=\frac{2\pi\cdot 3+2\pi\cdot 1}{3}=\frac{8\pi}{3}\\x_{3}=4\pi-\frac{\pi}{2}=\frac{4\pi\cdot 2-\pi}{2}=\frac{7\pi}{2}
Ответ: a)\frac{\pi}{2}+\pi n,n\in Z;\frac{\pi}{3}+2\pi k,k\in Z;\frac{2\pi}{3}+2\pi m,m\in Z \\б) \frac{5\pi}{2}; \frac{8\pi}{3};\frac{7\pi}{2}.
При решении использовал следствие (8) из формулы справочного материала ЕГЭ:
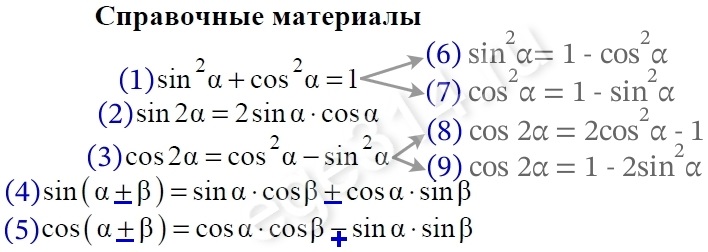
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 28
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.
