Около окружности описана трапеция, периметр которой равен 44. Найдите длину её средней линии.
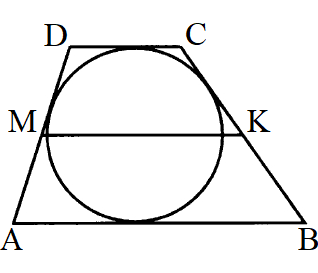
Дано:
ABCD – трапеция, описанная около окружности;
PABCD = 44
MK – средняя линия;
Найти: MK.
Решение:
Длина средней линии трапеции равна полусумме её оснований.
MK = \frac{DC + AB}{2}
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон равны.
DC + AB = DA + CB
То, зная PABCD, найдём сумму оснований DC и АВ:
PABCD = DC + AB + DA + CB = DC + AB + DC + AB = 2·(DC + AB) = 44
DC + AB = \frac{44}{2} = 22
Средняя линия MK равна:
MK = \frac{DC + AB}{2}=\frac{22}{2}=11
Ответ: 11.