Решение:
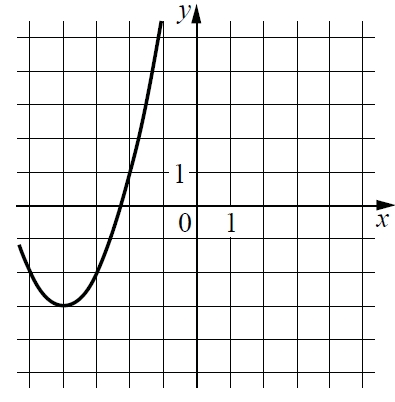
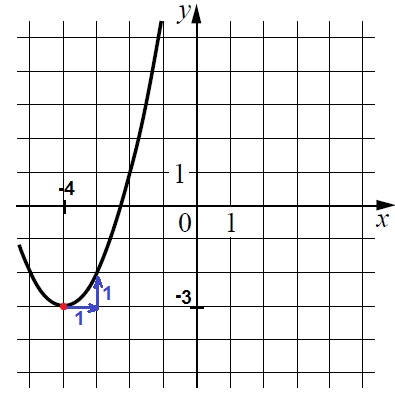
По графику видим, что у данной параболы коэффициент а = 1.
Вершина параболы находится в точке (–4; –3). Координата х вершины параболы находится по формуле:
x=\frac{–b}{2a}
Подставим известные значения и найдём b:
-4=\frac{–b}{2\cdot 1}\\-b=-4\cdot 2
b = 8
Подставив координаты вершины параболы х и у найдём коэффициент с:
y = ax2 + bx + c
–3 = 1·(–4)2 + 8·(–4) + c
–3 = 16 – 32 + c
c = 13
Функция имеет вид:
f(x) = 1·x2 + 8x + 13
Найдём f(−12):
f(–12) = 1·(–12)2 + 8·(–12) + 13 = 144 – 96 + 13 = 61
Ответ: 61.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 86
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.