Решение:
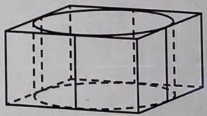
Правильной четырёхугольной призмой – называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками.
Площадь боковой поверхности данной призмы – это площадь 4-х равных прямоугольников.
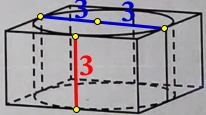
Длина прямоугольника равна диаметру цилиндра, ширина прямоугольника равна высоте цилиндра.
Найдём площадь боковой поверхности призмы:
Sбок. поверх. = 4·Sпрямоугольника = 4·h·(r + r) = 4·3·(3 + 3) = 4·3·6 = 72
Ответ: 72.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.4 / 5. Количество оценок: 95
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.