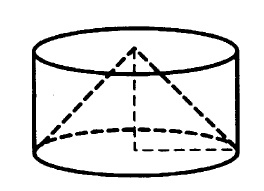
Решение:
По условию высота цилиндра равна радиусу основания:
h = R
Площадь боковой поверхности цилиндра по условию равна 27√2 и находится по формуле:
S_{бок. пов. цил.}=2\pi Rh=2\pi \cdot R\cdot R=2\pi R^{2}=27\sqrt{2}\\\pi R^{2}=\frac{27\sqrt{2}}{2}
Площадь боковой поверхности конуса по формуле:
S_{бок. пов. кон.}=\pi Rl
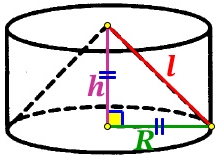
Из прямоугольного треугольника по теореме Пифагора найдём образующую конуса l:
l2 = h2 + R2
l2 = R2 + R2
l2 = 2R2
l = √2R
Подставим в формулу площади боковой поверхности конуса:
S_{бок. пов. кон.}=\pi R\cdot \sqrt{2}R=\sqrt{2}\pi R^{2}
Из формулы площади боковой поверхности цилиндра подставим значение πR2:
S_{бок. пов. кон.}=\sqrt{2}\cdot \pi R^{2}=\sqrt{2}\cdot \frac{27\sqrt{2}}{2}=\frac{27\cdot 2}{2}=27
Ответ: 27.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 6
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.