Решение №4210 Сумма двух углов равнобедренной трапеции равна 94°.

Решение:

    По условию сумма каких то двух углов трапеции равна 102°.

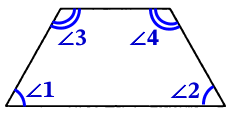
    Сумма углов ∠1 + ∠3 и ∠2 + ∠4 равна по 180°, как сумма односторонних углов при двух параллельных прямых и секущей.
    В равнобедренной трапеции углы при основаниях равны:

∠1 = ∠2
∠3 = ∠4

    Тогда из этого равенства, аналогично:

∠1 + ∠4 = 180°
∠2 + ∠3 = 180°

    Получается, что в условии дали сумму равных углов при каком то из оснований трапеции. Найдём чему равен каждый из них:

94º/2 = 47°

    Это острый угол, значит:

∠1 = 47°
∠2 = 47°

    Найдём тупые углы при верхнем основании (это и будет больший угол трапеции):

∠1 + ∠3 = 180°
47° + ∠3 = 180°
∠3 = 180 – 47° = 133°
∠3 = ∠4 = 133°

Ответ: 133.