Решение заданий Варианта №1 из сборника ОГЭ 2021 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
ЧАСТЬ 1
Задание 1-5.
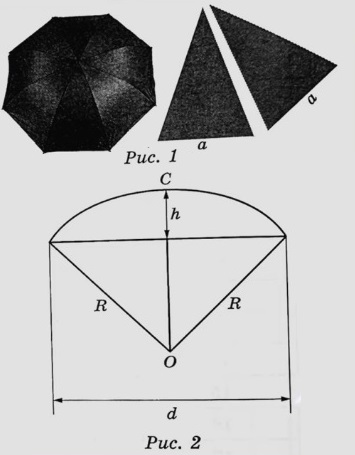
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 100 см.
Задание 6.
Найдите значение выражения \frac{9}{16}:(-\frac{3}{40})+4,7.
Задание 7.
Одно из чисел √28, √33, √38, √47 отмечено на прямой А.
Какое это число?
1)√28 2)√33 3)√38 4)√47
Задание 8.
Найдите значение выражения \frac{(a^{4})^{-3}}{a^{-15}} при а = 2.
Задание 9.
Найдите корень уравнения (х + 10)2 = (5 – х)2.
Задание 10.
В магазине канцтоваров продаётся 200 ручек: 31 красная, 25 зеленых, 38 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или черной.
Задание 11.
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
ФОРМУЛЫ
А) у = –4х2 – 28х – 46
Б) у = 4х2 – 28х + 46
С) у = –4х2 + 28х – 46
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле a = ω2R, где ω – угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 9 с-1, а центростремительное ускорение равно 243 м/с2. Ответ дайте в метрах.
Задание 13.
Укажите решение неравенства (х + 2)(х – 7) > 0
Задание 14.
В течение 20 банковских дней акции компании дорожали ежедневно на одну и ту же сумму. Сколько стоила акция компании в последний день этого периода, если в 9-й день акция стоила 888 рублей, а в 13-й день – 940 рублей?
Задание 15.
Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника.
Задание 16.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 38º, угол CAD равен 33º. Найдите угол ABD. Ответ дайте в градусах.
Задание 17.
Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Задание 19.
Какие из следующих утверждений верны?
1) Основания любой трапеции параллельны.
2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
3) Все углы ромба равны.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
ЧАСТЬ 2
Задание 20.
Решите уравнение x6 = – (12 – 8x)3
Задание 21.
Два велосипедиста одновременно отправились в 208-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым.
Задание 22.
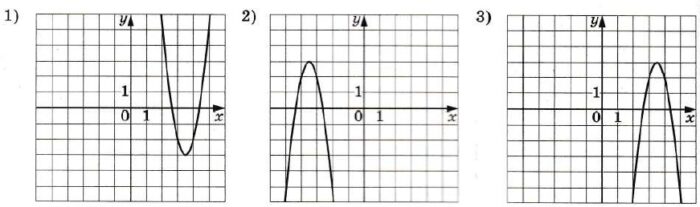
Постройте график функции у = х2 – 4|х| – х и определите, при каких значениях m прямая у = m имеет с графиком не менее одной, но не более трёх общих точек.
Задание 23.
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 6:13:17. Найдите радиус окружности, если меньшая из сторон равна 18.
Задание 24.
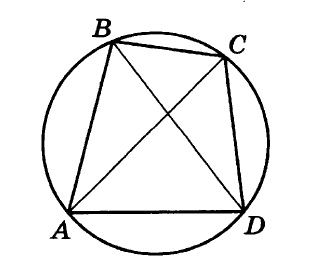
Основания ВС и АD трапеции АВСВ равны соответственно 5 и 45, BD = 15. Докажите, что треугольники СВD и ВDА подобны.
Задание 25.
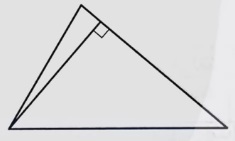
В треугольнике АВС на его медиане ВМ отмечена точка К так, что ВК : КМ = 6 : 7 Прямая АК пересекает сторону ВС в точке Р. Найдите отношение площади треугольника ВКР к площади треугольника АВК.
Источник варианта: Сборник ОГЭ 2021 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.