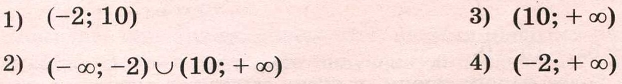Решение заданий варианта №5 из сборника ОГЭ 2021 по математике И.В. Ященко. ГДЗ для 9 класса.
ЧАСТЬ 1
Задание 1-5.
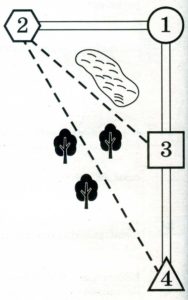
Миша летом отдыхает у дедушки и бабушки в деревне Николаевке. Миша с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Николаевки в Игнатьево можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Свистуху до деревни Берёзовки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Игнатьево. Есть и третий маршрут: в Свистухе можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Игнатьево.
По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Николаевки до Свистухи равно 16 км, от Николаевки до Берёзовки – 36 км, а от Берёзовки до Игнатьево 15 км.
Задание 6.
Найдите значение выражения 3,2 – 3,5·6,4
Задание 7.
Одно из чисел ,
,
,
отмечено на прямой точкой.
Какое это число?
1) 2)
3)
4)
Задание 8.
Найдите значение выражения при р = 5 и q = 2.
Задание 9.
Решите уравнение x2 + 8x + 15 = 0.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Задание 10.
В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Задание 11.
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Закон Джоуля – Ленца можно записать в виде , где Q – количество теплоты (в джоулях), I – сила тока (в амперах), R – сопротивление цепи (в омах), а t – время (в секундах). Пользуясь этой формулой, найдите сопротивление цепи R (в омах), если Q = 1296 Дж, I = 9 А, t = 2 c.
Задание 13.
Укажите решение неравенства (x + 2)(х – 10) > 0.
Задание 14.
В амфитеатре 20 рядов. В первом ряду 56 мест, а в каждом следующем – на 2 места меньше, чем в предыдущем. Сколько всего мест в амфитеатре?
Задание 15.
Точки М и N являются серединами сторон АВ и ВС треугольника АBС соответственно. Отрезки АN и СМ пересекаются в точке О, АN = 18, СМ = 21. Найдите ОМ.
Задание 16.
Угол А четырёхугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырёхугольника. Ответ дайте в градусах.
Задание 17.
Найдите площадь параллелограмма, изображённого на рисунке.
Задание 18.
На клетчатой бумаге с размером клетки 1 х 1 изображён ромб. Найдите длину его меньшей диагонали.
Задание 19.
Какое из следующих утверждений не верно?
1) Через заданную точку плоскости можно провести только одну прямую.
2) Все равносторонние треугольники подобны.
3) Сумма острых углов прямоугольного треугольника равна 90 градусам.
В ответ запишите номер выбранного утверждения.
ЧАСТЬ 2
Задание 20.
Решите неравенство
Задание 21.
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 51 минуту, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость второго – 20 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Задание 22.
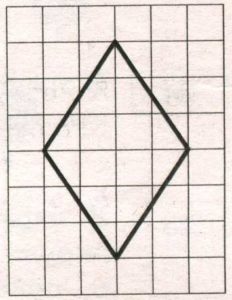
Постройте график функции и определите, при каких значениях m прямая у = m имеет с графиком ровно одну общую точку.
Задание 23.
Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АР = 34, а сторона ВС в 2 раза меньше стороны АВ.
Задание 24.
В треугольнике АВС с тупым углом АВС проведены высоты АА1 и CC1. Докажите, что треугольники А1ВС1 и АВС подобны.
Задание 25.
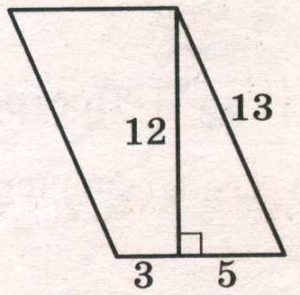
В параллелограмме АВСD проведена диагональ АС. Точка O является центром окружности, вписанной в треугольник АВС. Расстояния от точки O до точки А и прямых АD и АС соответственно равны 25, 15 и 7. Найдите площадь параллелограмма АВСD.
Источник варианта: Сборник ОГЭ 2021 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.