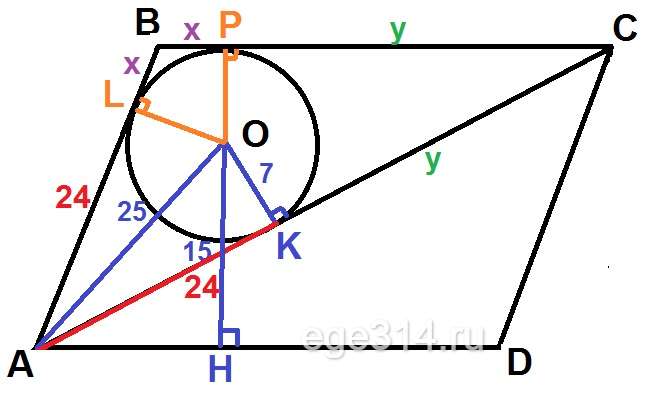
В параллелограмме АВСD проведена диагональ АС. Точка O является центром окружности, вписанной в треугольник АВС. Расстояния от точки O до точки А и прямых АD и АС соответственно равны 25, 15 и 7. Найдите площадь параллелограмма АВСD.
Источник: ОГЭ 2021 Ященко (36 вариантов)
Решение:
Параллелограмм АВСD делится диагональю АС на два равных треугольника. ΔАВС = ΔАDС, SABCD = 2·SABC
Площадь треугольника можно найти по двум формулам:
S_{\Delta }=\frac{1}{2}ah=\frac{a+b+c}{2}\cdot R
ОК = 7 – будет являться радиусом окружности и высотой к стороне АС, построим ещё два радиуса ОР и OL, которые будут являться высотами к BC и AB.
Отрезки ОР и ОН будут лежать на одной прямой НР (т.к. BC||AD, OP⊥BC, OH⊥AD), которая является высотой параллелограмма АВСD и высотой треугольника АВС к стороне ВС.
Найдём высоту НР:
НР = ОР + ОН = 7 + 15 = 22
Тогда площадь треугольника АВС по первой формуле равна:
S_{ABC}=\frac{1}{2}\cdot BC\cdot 22=11\cdot BC
По теореме Пифагора из прямоугольного треугольника найдём АК:
АК2 = АО2 – ОК2
АК2 = 252 – 72 = 576
АК = √576 = 24
Если окружность вписана в треугольник, то расстояния от вершины угла до точек касания окружности со сторонами угла равны:
АК = AL = 24
BL = BP = x
CP = CK = y
Отсюда стороны треугольника АВС равны:
АС = 24 + y
AB = 24 + x
BC = x + y
Площадь треугольника по второй формуле равна:
S_{\Delta}=p\cdot R\\S_{ABC}=\frac{AC+AB+BC}{2}\cdot OK=\frac{24+y+24+x+x+y}{2}\cdot 7=\frac{2\cdot (24+x+y)}{2}\cdot 7=(24+x+y)\cdot 7=(24+BC)\cdot 7
Приравняем оба выражения для нахождения площади:
11BC=(24+BC)\cdot 7\\11BC=7\cdot 24+7BC\\11BC-7BC=7\cdot 24\\4BC=7\cdot 24 {\color{Blue} |: 4}\\BC=7\cdot 6\\BC=42
Найдём площадь параллелограмма АВСD:
SABCD = 2·SABC = 2·11·BC = 22·42 = 924
Ответ: 924.