Решение заданий Варианта №10 из сборника ОГЭ 2022 по математике И.В. Ященко 36 типовых вариантов ФИПИ школе. ГДЗ решебник для 9 класса. Ответы с решением. Полный разбор всех заданий.
Начиная с варианта №9, на некоторые задания буду давать ссылки на решение такого же задания, но с другими числами (подобное задание). Для решения вам необходимо будет подставить числа из вашего задания.
Делаю это для того, чтобы успеть за этот учебный год решить больше вариантов ОГЭ. Тем более на экзамене вы должны будете уметь решить задание с любыми числами в условии.
Если какое-то, задание будет не понятно, или этот метод с ссылками на подобные задания вам не удобен, пишите в комментариях под вариантом.
ЧАСТЬ 1
Задание 1-5.
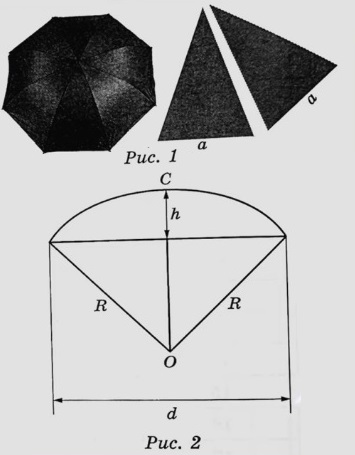
Две подруги Оля и Аня задумались о том, как рассчитать площадь поверхности зонта.
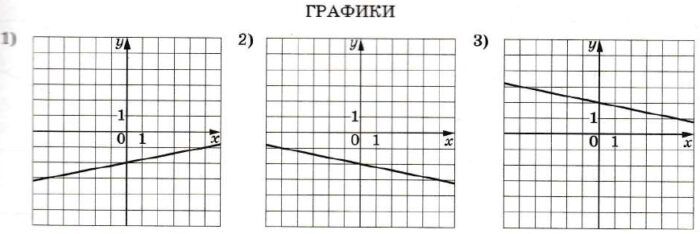
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт.
Оля и Аня сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 28 см. Высота купола зонта h (рис. 2) оказалась равна 27 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, – ровно 108 см.
Ответ задания №1: 60,6.
Ответ задания №2: 9910.
Ответ задания №3: 67,5.
Ответ задания №4: 11445.
Ответ задания №5: 15.
Задание 6.
Найдите значение выражения \frac{3}{4}-\frac{9}{20}:\frac{3}{7}.
Задание 7.
Какое из следующих чисел заключено между числами -\frac{8}{11} и -\frac{14}{17}?
1) –0,6 2) –0,7 3) –0,8 4) –0,9
В ответ запишите номер выбранного варианта.
Задание 8.
Найдите значение выражения \frac{24^{4}}{3^{2}\cdot 8^{3}}.
Задание 9.
Найдите корень уравнения 5х2 = 3х.
Если уравнение имеет более одного корня, в ответ запишите больший из корней.
Задание 10.
В девятом физико-математическом классе учатся 19 мальчиков и 6 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
Задание 11.
Установите соответствие между формулами, которыми заданы функции, и графиками этих функций.
ФОРМУЛЫ
А) у = \frac{1}{5}х – 2
Б) у = -\frac{1}{5}х + 2
С) у = -\frac{1}{5}х – 2
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Задание 12.
Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле v=\sqrt{2gh}. Найдите скорость (в м/с),с которой ударится о землю камень, падающий с высоты 90 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2.
Задание 13.
Укажите решение системы неравенств
\left\{\begin{matrix} -27+3x>0,\\ 6-3x<-6. \end{matrix}\right.
Задание 14.
Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 7 метров, а в каждую следующую секунду на 10 метров больше ,чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?
Задание 15.
В треугольнике АВС угол С равен 115°. Найдите внешний угол при вершине С. Ответ дайте в градусах.
Задание 16.
Хорды АС и ВD окружности пересекаются в точке Р, ВР = 12, СР = 6, DР = 13. Найдите АР.
Задание 17.
Диагонали АС и ВD трапеции АВСD с основаниями ВС и АD пересекаются в точке О, ВС = 4, АD = 9, АС = 26. Найдите АО.
Задание 18.
На клетчатой бумаге с размером клетки 1×1 изображен ромб. Найдите площадь этого ромба.
Задание 19.
Какое из следующих утверждений верно?
1) Площадь параллелограмма равна половине произведения его диагоналей.
2) Сумма углов прямоугольного треугольника равна 90 градусам.
3) Биссектрисы треугольника пересекаются в точке, которая является центром окружности, вписанной в этот треугольник.
В ответ запишите номер выбранного утверждения.
ЧАСТЬ 2
Задание 20.
Решите уравнение
\frac{1}{(x–2)^{2}}-\frac{1}{x–2}-6=0
Задание 21.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 112 км. На следующий день он отправился обратно в А, увеличив скорость на 9 км/ч. По пути он сделал остановку на 4 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А.
Задание 22.
Постройте график функции y=\frac{(x^{2}–4)(x^{2}–4x+3)}{(x^{2}–3x+2)} и определите, при каких значениях m прямая у = m имеет с графиком ровно одну общую точку.
Задание 23.
Биссектрисы углов А и В боковой стороне АВ трапеции АВСD пересекаются в точке F. Найдите АВ, если АF = 15, ВF = 8.
Задание 24.
В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
Задание 25.
Точки M и N лежат на стороне АС треугольника АВС на расстояниях соответственно 16 и 39 от вершины А. Найдите радиус окружности, проходящей через точки М и N и касающейся луча АВ, если cos∠BAC = \frac{\sqrt{39}}{8}.
Источник варианта: Сборник ОГЭ 2022 по математике. Типовые экзаменационные варианты. 36 вариантов. Под редакцией И.В. Ященко.