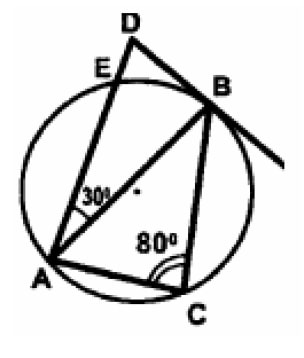
Найдите угол ADB (в градусах), изображенный на рисунке. Угол DAB равен 30º, угол АСВ равен 80º. DB – касательная к окружности.
Решение:
‿АВ = 360 – 2·∠АСВ = 360 – 2·80 = 360 – 160 = 200º
‿ЕВ = 2·∠ЕАВ = 2·30 = 60º
Угол ABD, образован касательной и секущей, он равен половине разности величин дуг, заключённых между его сторонами.
∠ABD = \frac{‿AB–‿EB}{2}=\frac{200°–60°}{2}=\frac{140°}{2} = 70º
Ответ: 70.