Решение и ответы заданий Варианта №3 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.
Задания №13,16 долго оформлять, решу их позже, если будет время и желание.
Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
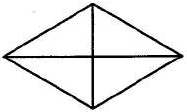
Площадь ромба равна 10. Одна из его диагоналей равна 8. Найдите другую диагональ.
Задание 2.
Длина окружности основания цилиндра равна 5, высота равна 6. Найдите площадь боковой поверхности цилиндра.
Задание 3.
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,83. Вероятность того, что окажется меньше 10 пассажиров, равна 0,46. Найдите вероятность того, что число пассажиров будет от 10 до 20.
Задание 4.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Биолог» выиграет жребий ровно два раза.
Задание 5.
Найдите корень уравнения cos\frac{\pi(2x–6)}{6}=\frac{\sqrt{3}}{2}. В ответе запишите наибольший отрицательный корень.
Задание 6.
Найдите значение выражения \frac{4^{4,75}}{8^{2,5}}.
Задание 7.
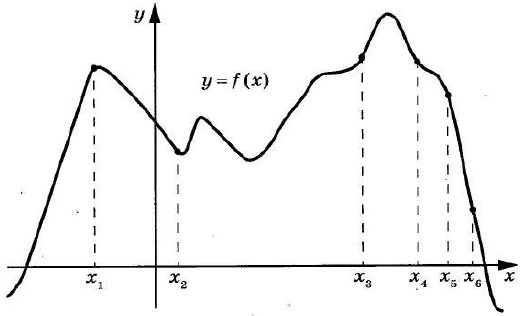
На рисунке изображён график функции y = f(x). На оси абсцисс отмечено шесть точек: x1, x2, x3, x4, x5, x6. В ответе укажите количество точек (из отмеченных) в которых производная функции f(x) положительна?
Задание 8.
Наблюдатель находится на высоте h, выраженной в метрах. Расстояние от наблюдателя до наблюдаемой им линии горизонта, выраженное в километрах, вычисляется по формуле l=\sqrt{\frac{Rh}{500}}, где R = 6400 км – радиус Земли. На какой высоте находится наблюдатель, если он видит линию горизонта на расстоянии 25,6 километра? Ответ дайте в метрах.
Задание 9.
Заказ на изготовление 238 деталей первый рабочий выполняет на 3 часа быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 3 детали больше?
Задание 10.
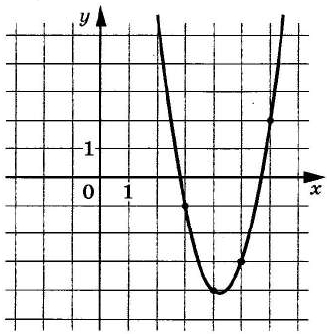
На рисунке изображён график функции f(x) = ax2 + bc + c. Найдите с.
Задание 11.
Найдите наибольшее значение функции y = ln(x + 18)12 − 12x на отрезке [−17,5;0].
Задание 12.
а) Решите уравнение 4^{x+\sqrt{x}–1,5}+3\cdot 4^{x–\sqrt{x}+1,5}-4^{x+1}=0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [2; 6].
Задание 13.
В прямой пятиугольной призме ABCDEA1B1C1D1E1, высота АА1, равна 3√5, BC = CD = 6, а четырехугольник ABDE прямоугольник со сторонами АВ = 5 и AE = 4√5.
а) Докажите, что плоскости СA1E1 и AED1 перпендикулярны.
б) Найдите объём многогранника CAED1B1.
Задание 14.
Решите неравенство logtg3,2 (log3 (9 – x2)) ≥ 0.
Задание 15.
В июле Максим планирует взять кредит в банке на некоторую сумму. Банк предложил Максиму два варианта кредитования.
1-й вариант:
– кредит предоставляется на 3 года;
– в январе каждого года действия кредита долг увеличивается на 20% от суммы долга на конец предыдущего года;
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платеж должен погасить долг по кредиту полностью,
2-й вариант:
– кредит предоставляется на 2 года:
– в январе каждого года действия кредита долг увеличивается на 24 %;
– в период с февраля по июнь каждого года действия кредита выплачиваются равные суммы, причём последний платёж должен погасить долг по кредиту полностью.
Когда Максим подсчитал, то выяснил, что по 1-му варианту кредитования ему придется выплачивать на 373 600 рублей больше, чем по 2-му варианту. Какую сумму Максим планирует взять в кредит?
Задание 16.
Четырёхугольник ABCD со сторонами ВС = 7 и AB = CD = 20 вписан в окружность радиусом R = 16.
а) Докажите, что прямые ВС и AD параллельны.
б) Найдите AD.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
\frac{log_{0,4}(6x^{2}–13x+5ax–6a^{2}–13a+6)}{\sqrt{2x–3a+4}}=0
имеет единственный корень.
Задание 18.
Все члены конечной последовательности являются натуральными числами. Каждый член этой последовательности, начиная со второго, либо в 7 раз больше, либо в 7 раз меньше предыдущего. Сумма всех членов последовательности равна 9177.
а) Может ли последовательность состоять из трёх членов?
б) Может ли последовательность состоять из пяти членов?
в) Какое наибольшее количество членов может быть в последовательности?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.