Решение и ответы заданий Варианта №2 из сборника ЕГЭ 2023 по математике (профильный уровень) И.В. Ященко. ГДЗ профиль для 11 класса. Полный разбор.
Задания №13,16 долго оформлять, решу их позже, если будет время и желание.
Решены те задания, у которых кнопка «Смотреть решение» зелёная.
Задание 1.
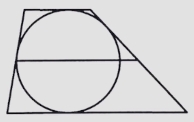
Около окружности описана трапеция, периметр которой равен 30. Найдите длину её средней линии.
Задание 2.
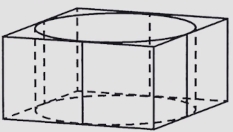
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 18,5. Объём параллелепипеда равен 5476. Найдите высоту цилиндра.
Задание 3.
Вероятность того, что на тестировании по химии учащийся П. верно решит больше 10 задач, равна 0,63. Вероятность того, что П. верно решит больше 9 задач, равна 0,75. Найдите вероятность того, что П. верно решит ровно 10 задач.
Задание 4.
При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше 810 г, равна 0,97. Вероятность того, что масса окажется больше 790 г, равна 0,94. Найдите вероятность того, что масса буханки больше 790 г, но меньше 810 г.
Задание 5.
Найдите корень уравнения log4 (7 + 6x) = log4 (1 + x) + 2.
Задание 6.
Найдите значение выражения \frac{2cos20^{\circ }\cdot cos70^{\circ }}{5sin40^{\circ }}.
Задание 7.
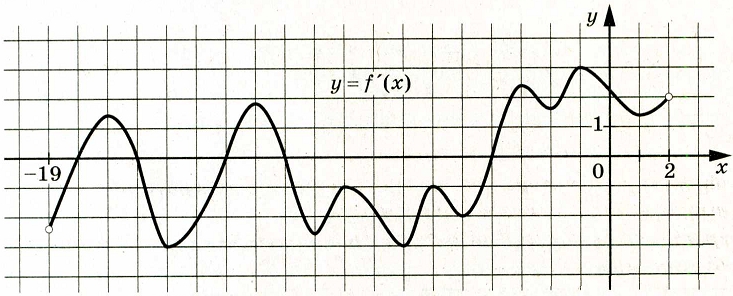
На рисунке изображён график y = f′(x) – производной функции f(x), определенной на интервале (−19; 2). Найдите количество точек максимума функции f(x), принадлежащих отрезку [–14; 0].
Задание 8.
При адиабатическом процессе для идеального газа выполняется закон pVk = 8,1·104 Па·м4, где p –давление в газе в паскалях, V – объём газа в кубических метрах, k = \frac{4}{3}. Найдите, какой объём V (в куб. м) будет занимать газ при давлении p, равном 6,25·105 Па.
Задание 9.
Моторная лодка прошла против течения реки 247 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна 3 км/ч. Ответ дайте в км/ч.
Задание 10.
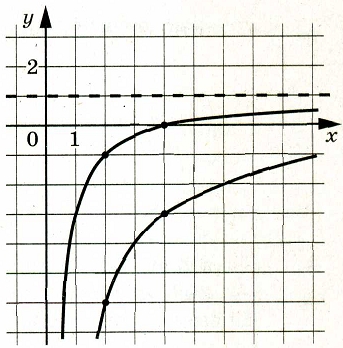
На рисунке изображены части графиков функций f(x)=\frac{k}{x} и g(x)=\frac{c}{x}+d. Найдите абсциссу точки пересечения графиков этих функций.
Задание 11.
Найдите точку максимума функции y = 15 + 21x – 4x√x.
Задание 12.
а) Решите уравнение sin2x – 2sin(–x) = 1 + cos(–x).
б) Найдите все корни этого уравнения, принадлежащие отрезку [-\frac{7\pi}{2};-2\pi].
Задание 13.
В основании пирамиды SABCD лежит трапеция ABCD с большим основанием AD. Диагонали пересекаются в точке O. Точки M и N – середины боковых сторон AB и CD соответственно. Плоскость α проходит через точки M и N параллельно прямой SO.
а) Докажите, что сечение пирамиды SABCD плоскостью α является трапецией.
б) Найдите площадь сечения пирамиды SABCD плоскостью α, если AD = 8,5, BC = 7,5, SO = 6,5, а прямая SO перпендикулярна прямой AD.
Задание 14.
Решите неравенство 5^{x}-10\ge \frac{225}{5^{x}–10}.
Задание 15.
В июле 2027 года планируется взять кредит на 3 года в размере 600 тыс. рублей. Условия возврата таковы:
– каждый январь действия кредита долг возрастает на 10% по сравнению с концом предыдущего года;
– с февраля по июнь необходимо выплатить часть долга;
– в 2028 и 2029 годах платежи по кредиту равные;
– в 2030 года выплачивается остаток по кредиту.
Найдите платёж 2029 года, если общие выплаты по кредиту составили 733,5 тыс. рублей.
Задание 16.
В параллелограмме ABCD угол BAC вдвое больше угла CAD. Биссектриса угла BAC пересекает отрезок BC в точке L. На продолжении стороны CD за точку D выбрана такая точка E, что AE = CE.
а) Докажите, что AB:AL = BC:AC.
б) Найдите EL, если AC = 24, tg∠BCA = 0,6.
Задание 17.
Найдите все значения a, при каждом из которых уравнение
2a2 + 3ax – 2x2 – 8a – 6x + 10|x| = 0
имеет четыре различных корня.
Задание 18.
Есть три коробки: в первой коробке 95 камней, во второй – 104, в третья – пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в третьей коробке оказаться 199 камней?
б) Могло ли в первой коробке оказаться 100 камня, во второй – 50, в третьей – 49?
в) В первой коробке оказалось 2 камня. Какое наибольшее число камней могло оказаться в третьей коробке?
Источник варианта: Сборник ЕГЭ 2023. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.