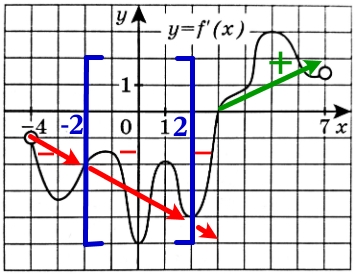
На рисунке изображён график y=f′(x) производной функции f(x), определенной на интервале (−4; 7). В какой точке отрезка [−2; 2] функция f(x) принимает наименьшее значение?
Решение:
Дан график производной функции. Это значит, там где производная отрицательна, функция убывает, а где производная положительна, функция возрастает.
На всём промежутке [−2; 2] производная отрицательна, а значит функция f(x) убывает. Наименьшее значение на промежутке [−2;2] будет в крайней правой точке х = 2.
Ответ: 2.