Решение №1986 Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.

Решение:

    Противоположные стороны прямоугольника равны:

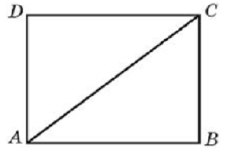
AD = BC
DC = AB

    1) Тогда периметр прямоугольника равен:

AD + BC + DC + AB = 28
AD + AD + DC + DC = 28
2AD + 2DC = 28
AD + DC = 14

    Из прямоугольного ΔADC по теорема Пифагора следует:

AD² + DC² = АС²
AD² + DC² = 100

    Подбором понимаем, что AD = 6, DC = 8, это единственные числа, сумма которых в квадрате равна ровно 100 (к такому же результату можно прийти решив систему уравнений).
    Найдём площадь прямоугольника:

S_▭ = AD·DC = 6·8 = 48

Ответ: 48.