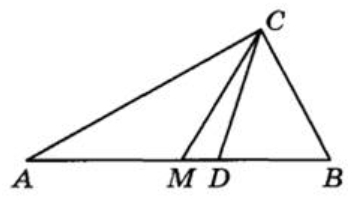
Решение:
ΔАВС прямоугольный ∠С = 90°, ∠В = 50°, найдём ∠А:
∠А = 180° – (90° + 50°) = 40°
Т.к. СМ – медиана, то по свойству медианы в прямоугольном треугольнике AМ = МВ = МС. Значит ΔAМС равнобедренный ∠А = ∠АСМ = 40°.
СD – биссектриса, делит прямой ∠С пополам.
Найдём ∠АСD:
∠АСD = ∠С/2 = 90°/2 = 45°
Найдём угол между биссектрисой и медианой:
∠MCD = ∠АСD – ∠АСМ = 45° – 40° = 5°
Ответ: 5.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.