Решение №1802 Найдите корень уравнения sin(π(x−3)/4)=√2/2.

Найдите корень уравнения $sin\frac{\pi(x-3) }{4}=\frac{\sqrt{2}}{2}$ .
В ответе запишите наименьший положительный корень.

Источник: mathege

Решение:

$sin\frac{\pi(x-3) }{4}=\frac{\sqrt{2}}{2}$

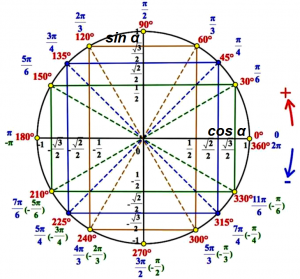
По тригонометрическому кругу определяем, в каких точках синус принимает значение равное $\frac{\sqrt{2}}{2}$ :

Синус равен $\frac{\sqrt{2}}{2}$ в точках:
1) $\frac{\pi }{4}+2\pi n,n\in \mathbb{Z}$

2) $\frac{3\pi }{4}+2\pi n,n\in \mathbb{Z}$ .

1 случай:

$\frac{\pi (x-3)}{4}=\frac{\pi }{4}+2\pi n$

Разделим обе части уравнения на π, получаем:

$\frac{x-3}{4}=\frac{1}{4}+2n$

Умножим обе части уравнения на 4, получаем:

x – 3 = 1 + 8n
x = 4 + 8n

n принимает только целые значения. Наименьший положительный корень в этом случае получим, если подставим n = 0.

n = 0, x = 4 + 8·0 = 4

2 случай:

$\frac{\pi (x-3)}{4}=\frac{3\pi }{4}+2\pi n$

Разделим обе части уравнения на π, получаем:

$\frac{x-3}{4}=\frac{3}{4}+2n$

Умножим обе части уравнения на 4, получаем:

x – 3 = 3 + 8n
x = 6 + 8n

n = 0, x = 6 + 8·0 = 6

В итоге наименьший положительный корень равен 4.

Ответ: 4.