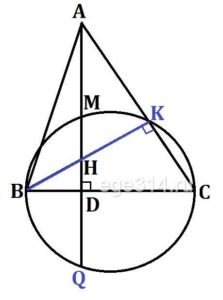
На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту АD в точке М, АD = 80‚ МD = 64, Н – точка пересечения высот треугольника АВС. Найдите АН.
Источник: ОГЭ 2021 Ященко (36 вар)
Решение:
Построим высоту BK, ВК⊥АС, ΔВKC прямоугольный и опирается на диаметр окружности, значит точка К лежит на окружности.
MQ – хорда окружности, диаметр ВС⊥MQ, значит хорда делится пополам в точке D:
MD = DQ = 64
Найдём АМ:
AM = AD – MD = 80 – 64 = 16
Найдём AQ:
AQ = AD + DQ = 80 + 64 = 144
По теореме о секущих:
AK·AC = AM·AQ
AK·AC = 16·144
ΔAKH и ΔADC подобны по двум углам: ∠AKH = ∠ADC = 90°, а ∠CAD – общий. Тогда стороны тоже подобны:
\frac{AK}{AH}=\frac{AD}{AC}\\AK\cdot AC=AH\cdot AD\\16\cdot 144=AH\cdot 80\\AH=\frac{16\cdot 144}{80}=28,8
Ответ: 28,8.