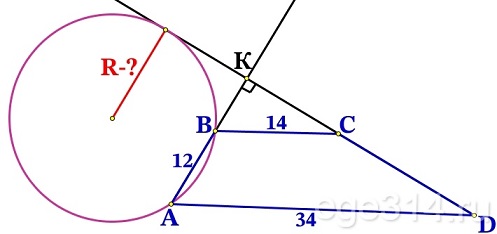
В трапеции АВСD основания АD и ВС равны соответственно 34 и 14, а сумма углов при основании АD равна 90°. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой СD, если АВ = 12.
Источник: ОГЭ 2021 Ященко (36 вар)
Решение:
Продолжим касательную CD и прямую АВ они пересекутся в какой то точке К.
По условию ∠А + ∠D = 90°, в треугольнике сумма 3-х углов равна 180°, тогда в ΔAKD ∠K = 180° – 90° = 90°, значит треугольник прямоугольный.
Треугольники ΔAKD и ΔBKC подобны по двум углам, в них ∠К общий, ∠KAD = ∠KBC как соответственные при BC||AD и секущей AB. Запишем пропорциональные стороны и найдём КB:
\frac{BC}{AD}=\frac{KB}{BA}\\\frac{14}{34}=\frac{KB}{KB+12}\\\frac{7}{17}=\frac{KB}{KB+12}\\7\cdot (KB+12)=17\cdot KB\\7\cdot KB+84=17\cdot KB\\84=17\cdot KB-7\cdot KB\\84=10\cdot KB\\KB=\frac{84}{10}=8,4
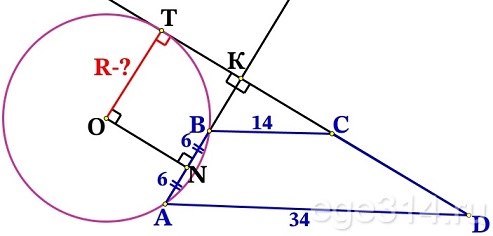
Проведём радиус ОT к касательной, ОT⊥DK.
Проведём перпендикулярную прямую ON к хорде AB, она будет делить АВ на два равных отрезка, найдём NB:
NB=\frac{AB}{2}=\frac{12}{2}=6
В четырёхугольнике NKTO три прямых угла, значит и 4-й угол прямой. Получаем, что это прямоугольник, противоположные стороны равны. Радиус OT равен:
OT = NK = NB + BK = 6 + 8,4 = 14,4
Ответ: 14,4.