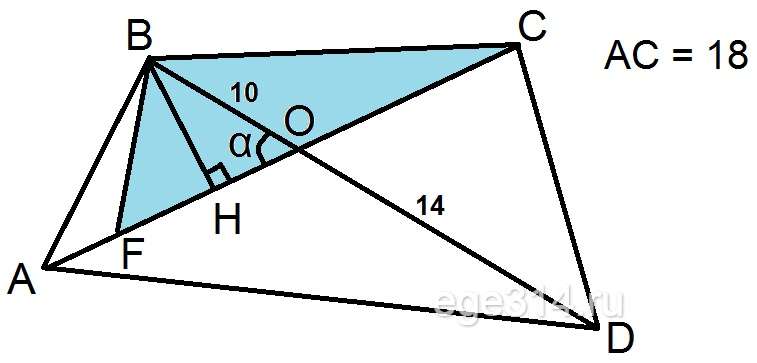
В четырёхугольнике АВСD диагонали пересекаются в точке O под углом α. Точка F принадлежит отрезку АС. Известно, что ВО = 10, DO = 14, АС = 18. Найдите АF, если площадь треугольника FВС в четыре раза меньше площади четырёхугольника АВСD.
Источник: ОГЭ 2021 Ященко 36 вариантов.
Решение:
Площадь четырёхугольника АВСD c диагоналями АС = 18 и BD = BO + DO = 10 + 14 = 24, находится по формуле:
SАBCD = \frac{1}{2}·АC·BD·sinα = \frac{1}{2}·18·24·sinα = 216·sinα
(1) По условию задачи площадь ΔFBC равна:
SFBC = \frac{1}{4}·SАBCD = \frac{1}{4}·216·sinα = 54·sinα
Площадь ΔFBC можно вычислить по другой формуле:
SFBC = \frac{1}{2}·FC·BH
Из прямоугольного ΔВHO найдём ВН:
sin\alpha=\frac{BH}{BO}\\sin\alpha=\frac{BH}{10}\\BH=10\cdot sin\alpha
(2) Подставим в формулу площади ΔFBC:
SFBC = \frac{1}{2}·FC·10·sinα = 5·FC·sinα
Прировняем две формулы (1) и (2), найдём FC:
54·sinα = 5·FC·sinα |:sinα
54 = 5·FC
FC=\frac{54}{5}=10,8
Найдём AF:
AF = AC – FC = 18 – 10,8 = 7,2
Ответ: 7,2.