Основания ВС и АD трапеции АВСВ равны соответственно 12 и 75, АС = 30. Докажите, что треугольники СВА и АСD подобны.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
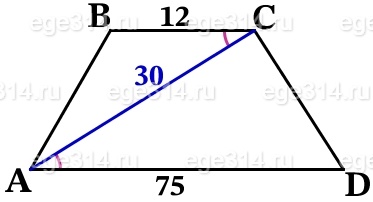
Требуется доказать, что ΔСВA ∼ ΔACD.
Рассмотрим эти треугольники.
В них ∠CAD = ∠ACB, как внутренне накрест лежащие при двух параллельных прямых AD и ВС и секущей AC.
В ΔСВA:
\frac{BC}{AC}=\frac{12}{30}=0,4
В ΔАCD:
\frac{AC}{AD}=\frac{30}{75}=0,4
Значит эти две стороны пропорциональны в двух треугольниках, т.к. имеют один коэффициент подобия 0,4.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны. ΔСВA ∼ ΔACD.
Что и требовалось доказать.