Решение №1604 В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке Р.

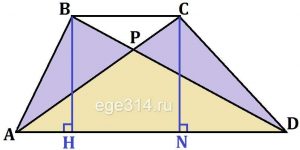
В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке Р. Докажите, что площади треугольников АРВ и СРD равны.

Источники: Основная волна ОГЭ 2022, ОГЭ 2021 Ященко (36 вар)

Решение:

Рассмотрим два других треугольника ΔАDB и ΔАDС. Докажем, что их площади равны. У них общее основание АD. В каждом из них проведём высоты ВН и CN они будут равны как высоты трапеции.

$S_{ADB}=\frac{1}{2}\cdot AD\cdot BH\\S_{ADC}=\frac{1}{2}\cdot AD\cdot CN$

Т.к. высоты CN = BH, то S_ADB = S_ADC. Площади ΔАРВ и ΔСРD можно получить отняв от площадей треугольников S_ADB = S_ADC площадь треугольника ΔАPD:

S_АРВ = S_ADB – S_АPD
S_СРD = S_ADC – S_АPD

Т.к. S_ADB = S_ADC, то и S_АРВ = S_СРD.
Что и требовалось доказать.