Решение №1341 Высоты BB1 и СС1 остроугольного треугольника АBС пересекаются в точке Е.

Решение:

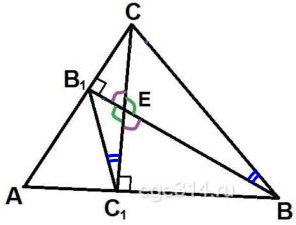
    Рассмотрим ΔВ₁ЕС и ΔС₁ЕВ в них ∠ЕВ₁С = ∠ЕС₁В, как прямые. ∠СЕВ₁ = ∠ВЕС₁, как вертикальные. Значит треугольники подобны по двум равным углам.
    В подобных треугольниках соответственные стороны пропорциональны, запишем соотношение:

\frac{EB_{1}}{EC_{1}}=\frac{EC}{EB}

    Рассмотрим ΔВ₁ЕС₁ и ΔСЕВ в них две стороны пропорциональны ЕВ₁∼ЕС₁, ЕС∼ЕВ, углы ∠В₁ЕС₁ = ∠СЕВ как вертикальные. Треугольники подобны по двум пропорциональным сторонам и равным углам между ними.
    Из подобия треугольников следует равенство углов:

∠СС₁В₁ = ∠СВВ₁

    Что и требовалось доказать.