Отрезки АВ и СD являются хордами окружности. Найдите длину хорды СD, если АВ = 24, а расстояние от центра окружности до хорд АВ и CD равны соответственно 16 и 12.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
Расстояния от центра окружности О до хорд АВ и CD это перпендикуляры ОН и ОК соответственно:
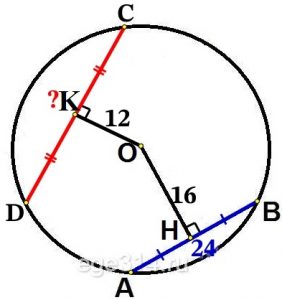
Построим радиусы ОВ и ОА, ΔАОВ равнобедренный, ОН является высотой, медианой и биссектрисой. Значит АН = НВ.
Найдём НВ:
НВ = АВ/2 = 24/2 = 12
ΔОНВ прямоугольный из него по теореме Пифагора найдём радиус ОВ:
OB=\sqrt{OH^{2}+HB^{2}}=\sqrt{16^{2}+12^{2}}=\sqrt{256+144}=\sqrt{400}=20
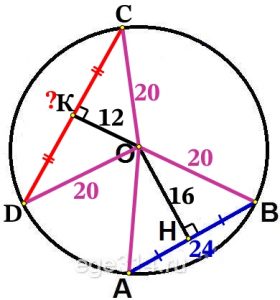
Аналогично, построим радиусы OC, OD. Получаем равнобедренный ΔCOD с высотой и медианой ОК.
ΔОКC прямоугольный из него по теореме Пифагора найдём KС:
KC=\sqrt{OC^{2}–KO^{2}}=\sqrt{20^{2}–12^{2}}=\sqrt{400–144}=\sqrt{256}=16
Найдём длину хорды СD:
CD = KC·2 = 16·2 = 32
Ответ: 32.