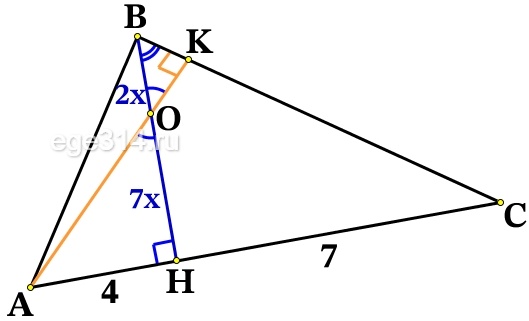
Высота треугольника разбивает его основание на два отрезка с длинами 4 и 7. Найдите длину этой высоты, если известно, что другая высота треугольника делит её в отношении 2:7, считая от вершины.
Источник: ОГЭ Лысенко 2022 (40 вар)
Решение:
Высота ВН делит основание АС на АН = 4 и НС = 7.
Высота АК делит высоту ВН на ВО = 2х и ОН = 7х, тогда ВН = 2х + 7х = 9х.
ΔАНО подобен ΔВКО, т.к. ∠АНО = ∠ВКО = 90°, ∠АОН = ∠ВОК как вертикальный. Запишем отношение пропорциональных сторон треугольников:
ΔBHC подобен ΔВКО, т.к. ∠BHC = ∠ВКО = 90°, ∠B – общий. Запишем отношение пропорциональных сторон треугольников:
В каждой пропорции возьмём последние две дроби и выразим из них KO:
Приравняем значения КО:
|: 7BK
x·9x = 4
9x2 = 4
x2 = \frac{4}{9}
x=\sqrt{\frac{4}{9}}=\frac{2}{3}
Зная х найдём искомую высоту ВН:
ВН = 9х = 9\cdot \frac{2}{3} = 3·2 = 6
Ответ: 6.