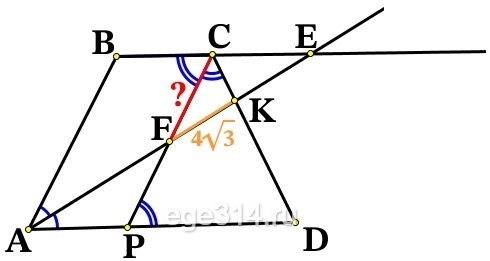
Решение №2250 В равнобедренной трапеции ABCD с большим основанием AD биссектриса угла А пересекается с биссектрисой угла С в точке F, а также пересекает сторону CD в точке К.

Решение:*

    ABCD – равнобедренная трапеция, углы при основаниях равны, сумма соседних (односторонних) углов равна 180°:

∠В = ∠С
∠А + ∠В = 180°

    Отсюда:

∠А + ∠С = 180°

    AK и CF – биссектрисы, делят углы пополам, тогда:

\frac{\angle A}{2}+\frac{\angle C}{2}=\frac{180°}{2}
∠KAD + ∠DCF = 90°

    По условию  АВ||CP, следовательно, ∠ВАF = ∠CFK, как соответственные, ∠ВАF = ∠KAD, как образованные биссектрисой, тогда:

∠CFK + ∠KCF = 90°

    Тогда в ΔСАK найдём ∠FKC:

∠FKC = 180 – (∠CFK + ∠KCF) = 180° – 90° = 90°

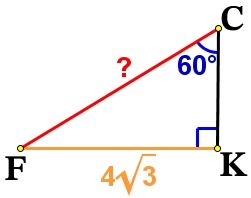
    Получаем прямоугольный ΔCFK с гипотенузой CF и прямым углом ∠К = 90°.

    E точка пересечении прямых AK и BC, углы ∠FAD = ∠CEK, как накрест лежащие углы, следовательно, ΔCFE – равнобедренный (CF = CE) с высотой CK. Значит, CK также и биссектриса, получаем:

∠ВСF = ∠FCK = ∠KCE = 180°/3 = 60°

    Рассмотрим прямоугольный ΔFCK с углом ∠C = 60º и стороной FK = 4√3.

    Через синус угла С найдём искомую сторону СF:

sin\angle C=\frac{FK}{FC}\\sin60°=\frac{4\sqrt{3}}{FC}\\\frac{\sqrt{3}}{2}=\frac{4\sqrt{3}}{FC}

    Разделим обе части на √3:

\frac{1}{2}=\frac{4}{FC}
FC = 2·4 = 8

Ответ: 8.