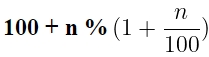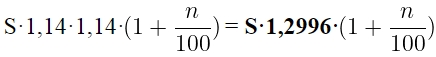По вкладу «А» банк в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» – увеличивает эту сумму на 14 % в течение каждого из первых двух лет. Найдите наименьшее натуральное число процентов, начисленное за третий год по вкладу «Б», при котором за все три года этот вклад будет более выгоден, чем вклад «А».
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
Пусть на вклады «А» и «Б» было внесено по S (100%) рублей.
Вклад «А» увеличивается каждый год в течении 3 лет на 10%, т.е. вклад в конце каждого года становится равным:
100 + 10 = 110% (1,1)
Через 3 года на вкладе «А» будет:
S·1,1·1,1·1,1 = S·1,331 рулей
Вклад «Б» увеличивается каждый год в течении 2 лет на 14%, т.е. вклад в конце каждого года становится равным:
100 + 14 = 114% (1,14)
В 3-й год вклад увеличился на n%, тогда вклад в конце года стал равен:
Через 3 года на вкладе «Б» будет:
По условию на вкладе «Б» через 3 года, должно быть больше денег, чем на вкладе «А», и при этом найти наименьший процент n в 3-й год:
Наименьшее целое n принадлежащее этому неравенству – это 3%.
Ответ: 3.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.7 / 5. Количество оценок: 34
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.