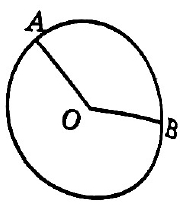
На окружности с центром О отмечены точки А и В так, что ∠АОВ = 122°. Длина меньшей дуги АВ равна 61. Найдите длину большей дуги АВ.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
∠АОВ равный 112° опирается на меньшую дугу ‿АВ, равную 61. Значит 1° в данной окружности соответствует:
\frac{61}{122} ед. длины дуги
Большая дуга ‿АВ соответствует центральному углу:
360° – 122° = 238°
Длина большей дуги равна:
\frac{61}{122}\cdot 238=\frac{61\cdot 238}{122}=\frac{1\cdot 238}{2}=119
Ответ: 119.