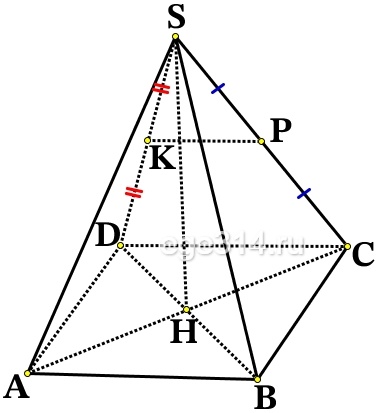
В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка К – середина бокового ребра SD. Плоскость АКВ пересекает боковое ребро SC в точке Р.
а) Докажите, что площадь четырёхугольника CDKP составляет \frac{3}{4} площади треугольника SCD.
б) Найдите объем пирамиды ACDKP.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
а) В основании правильной пирамиды лежит квадрат, тогда АВ||DC ⇒ AB|| плоскости SDC (признак параллельности прямой и плоскости).
Точка K∈ плоскости АКВ, которая пересекает плоскость SDC по прямой KP, тогда KP||AB ⇒ KP||DC ⇒ KP – средняя линяя ΔSDC (по теореме Фалеса).
ΔSDC подобен ΔSKP, т.к. ∠S – общий, \frac{SK}{SD}=\frac{KP}{DC}=\frac{1}{2}. Коэффициент подобия равен k = \frac{1}{2}.
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия:
\frac{S_{\Delta SKP}}{S_{\Delta SDC}}=k^{2}=(\frac{1}{2})^{2}=\frac{1}{4}
Отсюда:
S_{\Delta SKP}=\frac{1}{4}\cdot S_{\Delta SDC}
Тогда:
SCDKP = SΔSDC – SΔSKP = SΔSDC – \frac{1}{4}S_{\Delta SDC} = \frac{3}{4}·SΔSDC
Что и требовалось доказать.
б) Искомая пирамида ACDKP и пирамида АSDC имеют одну и туже высоту АО.
VASDC = VSADC (одна и таже пирамида)
VSADC = \frac{1}{3}SH·SADC = \frac{1}{3}·12·\frac{1}{2}·AD·DC = \frac{1}{3}·12·\frac{1}{2}·10·10 = \frac{1}{3}·12·50 = 200
Пирамиды ACDKP и АSDC отличаются только основаниями:
SCDKP = \frac{3}{4}·SΔSDC
Тогда:
VACDKP = \frac{3}{4}·VSADC = \frac{3}{4}·200 = 150
Ответ: 150.