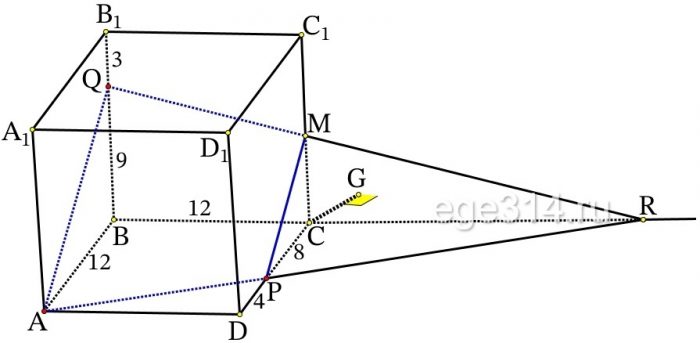
Решение №2045 На рёбрах CD и BB1 куба ABCDA1B1C1D1 с ребром 12 отмечены точки P и Q соответственно, причём DP = 4, а B1Q = 3. Плоскость APQ пересекает ребро CC1 в точке M.

Решение:

    а) Пусть прямые АР и ВС пересекаются в точке R:

    Ребра куба равны 12, найдём отрезки:

РС = DC – PD = 12 – 4 = 8
BQ = BB₁ – B₁Q = 12 – 3 = 9

    ΔABR подобен ΔPCR по двум равным углам (∠В = ∠С – прямые углы, ∠R – общий), отсюда:

\frac{AB}{CP}=\frac{BR}{CR}\\\frac{12}{8}=\frac{BC+CR}{CR}\\\frac{3}{2}=\frac{12+CR}{CR}
3CR = 24 + 2CR
CR = 24

    Найдём BR:

BR = BC + CR = 12 + 24 = 36

    ΔQBR подобен ΔMCR по двум равным углам (∠В = ∠С – прямые углы, ∠R – общий), отсюда:

\frac{QB}{MC}=\frac{BR}{CR}\\\frac{9}{MC}=\frac{36}{24}\\\frac{9}{MC}=\frac{3}{2}
3·MC = 2·9
МС = 6 тогда:
МС₁ = СС₁ – МС = 12 – 6 = 6

    МС = МС₁ ⇒ точка М середина СС₁
    Что и требовалось доказать.

    б) Расстояние от точки С до плоскости АPQ можно найти как высоту CG пирамиды СMPR выразив объём двумя способами:

V_{CMPR}=\frac{1}{3}\cdot S_{CMP}\cdot CR=\frac{1}{3}\cdot S_{MPR}\cdot CG

    По теореме Пифагора из прямоугольных ΔСМР, ΔСМR, СPR найдём стороны РМ, МR, PR соответственно:

PM=\sqrt{8^{2}+6^{2}}=\sqrt{100}=10\\MR=\sqrt{6^{2}+24^{2}}=\sqrt{612}=\sqrt{36\cdot 17}=6\sqrt{17}\\PR=\sqrt{8^{2}+24^{2}}=\sqrt{640}=\sqrt{64\cdot 10}=8\sqrt{10}

    По теореме косинусов:

MR² = PM² + RP² – 2·PM·RP·cos∠MPR
(6\sqrt{17})² = 10² +(8\sqrt{10})² – 2·10·8\sqrt{10}·cos∠MPR
612 = 100 + 640 – 2·10·8\sqrt{10}·cos∠MPR
2·10·8\sqrt{10}·cos∠MPR = 100 + 640 – 612
2·10·8\sqrt{10}·cos∠MPR = 100 + 640 – 612
160\sqrt{10}·cos∠MPR = 128
cos\angle MPR=\frac{128}{160\sqrt{10}}=\frac{4}{5\sqrt{10}}

    По основному тригонометрическому тождеству: 

cos²∠MPR + sin²∠MPR = 1
sin\angle MPR=\sqrt{1-cos^{2}\angle MPR}=\sqrt{1-(\frac{4}{5\sqrt{10}})^{2}}=\sqrt{1-\frac{16}{250}}=\sqrt{\frac{234}{250}}=\sqrt{\frac{117}{125}}

    Найдём СG:

\frac{1}{3}\cdot \frac{1}{2}\cdot CP\cdot CM\cdot CR=\frac{1}{3}\cdot \frac{1}{2}\cdot MP\cdot PR\cdot sin\angle MPR\cdot CG\\\frac{1}{3}\cdot \frac{1}{2}\cdot 8\cdot 6\cdot 24=\frac{1}{3}\cdot \frac{1}{2}\cdot 10\cdot 8\sqrt{10}\cdot \sqrt{\frac{117}{125}}\cdot CG\\6\cdot 24=10\sqrt{10}\cdot \sqrt{\frac{117}{125}}\cdot CG\\3\cdot 24=5\sqrt{10}\cdot \sqrt{\frac{117}{125}}\cdot CG\\72=5\cdot \sqrt{\frac{1170}{125}}\cdot CG\\72=5\cdot \frac{\sqrt{1170}}{5\sqrt{5}}\cdot CG\\72= \frac{\sqrt{1170}}{\sqrt{5}}\cdot CG\\72=\sqrt{234}\cdot CG\\CG=\frac{72}{\sqrt{9\cdot 26}}\\CG=\frac{72}{3\sqrt{26}}\\CG=\frac{24}{\sqrt{26}}=\frac{24\sqrt{26}}{26}=\frac{12\sqrt{26}}{13}

    Расстояние от точки C до плоскости APQ равно \frac{12\sqrt{26}}{13}.

Ответ: \frac{12\sqrt{26}}{13}.