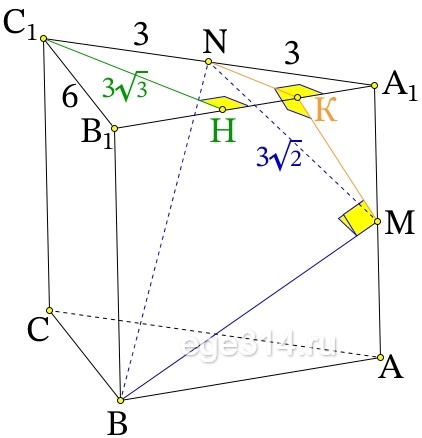
Решение №1958 Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N – середины рёбер AA1 и A1C1 соответственно.

Решение:

    а) Правильная треугольная призма – это треугольная призма у которой основания правильные треугольники, а боковые грани прямоугольники. Поэтому, все углы между основаниями и боковыми гранями прямые, равны 90°.
    Проведём BN, получаем ΔBNM, по обратной теореме Пифагора, докажем, что он прямоугольный, а значит BM⊥MN.

    Найдём стороны данного треугольника. C₁N = NA₁ = A₁M = MA = 3, т.к. точки N и M середины рёбер длинной 6.
    Сторону MN найдём из прямоугольного ΔMA₁N по теореме Пифагора:

MN=\sqrt{NA_{1}^{2}+A_{1}M^{2}}=\sqrt{3^{2}+3^{2}}=\sqrt{2\cdot 9}=3\sqrt{2}

    Сторону MB найдём из прямоугольного ΔMAB по теореме Пифагора:

MB=\sqrt{MA^{2}+BA^{2}}=\sqrt{3^{2}+6^{2}}=\sqrt{45}=\sqrt{9\cdot 5}=3\sqrt{5}

    В₁N делит противоположную сторону на равные отрезки в равностороннем треугольнике, она является медианой, высотой, биссектрисой. Найдём В₁N по теореме Пифагора из прямоугольного ΔNA₁B₁:

B_{1}N=\sqrt{B_{1}A_{1}^{2}-NA_{1}^{2}}=\sqrt{6^{2}-3^{2}}=\sqrt{27}=\sqrt{9\cdot 3}=3\sqrt{3}

    Сторону BN найдём из прямоугольного ΔBB₁N по теореме Пифагора:

BN=\sqrt{B_{1}B^{2}+B_{1}N^{2}}=\sqrt{6^{2}+(3\sqrt{3})^{2}}=\sqrt{63}=\sqrt{9\cdot 7}=3\sqrt{7}

    По обратной теореме Пифагора проверим, является ли ΔBNM прямоугольным: 

BN² = BM² + MN²
 (3\sqrt{7})^{2}=(3\sqrt{5})^{2}+(3\sqrt{2})^{2}
63 = 45 + 18
63 = 63 – верно

    Значит треугольник прямоугольный, ∠NMB = 90° (лежащий на против большей стороны, гипотенузы) ⇒ BM⊥MN.
    Что и требовалось доказать.

    б) Угол между плоскостями – это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
    Линия пересечения этих плоскостей – это прямая BM. Перпендикуляр из плоскости BMN –  это прямая MN, MN⊥BM – по доказанному в пункте а).
    Докажем, что перпендикуляр из плоскости АВВ₁ к ВM – это прямая КМ:

    Проведём перпендикуляр NK⊥B₁A₁ и отрезок КM. Так же NK⊥A₁A, т.к. у нас правильная треугольная призма. Значит NK перпендикулярна всей плоскости АВВ₁, т.к. она перпендикулярна двум пересекающимся прямым в этой плоскости ⇒ ∠NKM = 90°.
    Поэтому MK – проекция MN на плоскость ABB₁. Прямая BM⊥MN, тогда по теореме о трёх перпендикулярах BM⊥MK.
    Следовательно, искомый угол – это угол ∠NMK между перпендикулярами к прямой BM.
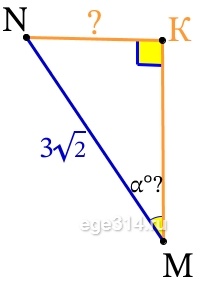
    ∠NMK находится в прямоугольном ΔNMK:

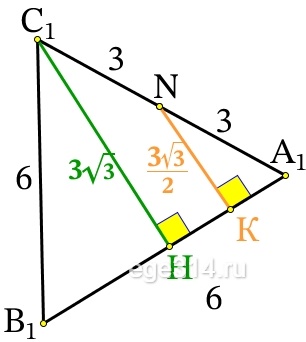
    Найдём его катет из равностороннего ΔА₁В₁С₁:

    Проведём в нём высоту С₁Н, она равна высоте В₁N = 3√3 из пункта а). NK – средняя линия треугольника, т.к. NK⊥В₁А₁ и N – cередина С₁А₁. Средняя линия треугольника равна половине параллельного основания:

NK=\frac{3\sqrt{3}}{2}

    Тогда в прямоугольном ΔNMK, найдём искомый угол, через синус угла:

sin\angle NMK=\frac{NK}{NM}=\frac{\frac{3\sqrt{3}}{2}}{3\sqrt{2}}=\frac{3\sqrt{3}}{2\cdot 3\sqrt{2}}=\frac{\sqrt{3}}{2\sqrt{3}}=\frac{\sqrt{3}}{\sqrt{8}}=\sqrt{\frac{3}{8}}\\\angle NMK=arcsin\sqrt{\frac{3}{8}}

Ответ: б)arcsin\sqrt{\frac{3}{8}}.