Найдите точку минимума функции y=–\frac{x}{x^{2}+256}.
Источники: fipi, os.fipi, Демо 2020
Решение:
y=\frac{–x}{x^{2}+256}
Найдем производную функции:
y^{′}=\frac{(–x)^{′}\cdot (x^{2}+256)–(–x)\cdot (x^{2}+256)^{′}}{(x^{2}+256)^{2}}=\frac{–(x^{2}+256)+2x^{2}}{(x^{2}+256)^{2}}=\frac{x^{2}–256}{(x^{2}+256)^{2}}
Найдем нули производной:
\frac{x^{2}–256}{(x^{2}+256)^{2}}=0
Знаменатель всегда положительный и на знак производной не влияет, отбросим его.
x2 – 256 = 0
x2 = 256
x = ±√256 = ±16
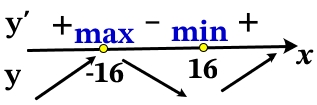
Определим знаки производной функции и изобразим поведение функции:
Точка минимума: х = 16.
Ответ: 16.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 47
Оценок пока нет. Поставь оценку первым.
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, чтобы я тебе ответил.