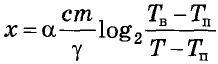Для обогрева помещения, температура в котором поддерживается на уровне Тп = 20 °C, через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды m = 0,5 кг/с. Проходя по трубе расстояние х, вода охлаждается от начальной температуры Тв = 72 °C до температуры Т, причём
где с = 4200 Вт·с/кг·°C – теплоёмкость воды, γ = 63 Вт/м·°C – коэффициент теплообмена, а α = 1,5 – постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 100 м.
Источник: Ященко ЕГЭ 2022 (36 вар)
Решение:
Тп = 20 °C,
m = 0,5 кг/с,
Тв = 72 °C,
с = 4200 Вт·с/кг·°C,
γ = 63 Вт/м·°C,
α = 1,5,
x = 100 м,
Т – ? °C.
Подставим все значения в формулу и найдём Т:
100=1,5\cdot \frac{4200\cdot 0,5}{63}\cdot log_{2}\frac{72–20}{T–20}\\100=\frac{1,5\cdot 420\cdot 5}{63}\cdot log_{2}\frac{52}{T–20}\\100=\frac{15\cdot 42\cdot 5}{63}\cdot log_{2}\frac{52}{T–20}\\100=\frac{5\cdot 42\cdot 5}{21}\cdot log_{2}\frac{52}{T–20}\\100=5\cdot 2\cdot 5\cdot log_{2}\frac{52}{T–20}\\100=50\cdot log_{2}\frac{52}{T–20}\\2=log_{2}\frac{52}{T–20}\\2^{2}=\frac{52}{T–20}\\\frac{4}{1}=\frac{52}{T–20}
4·(Т – 20) = 1·52
4Т – 80 = 52
4Т = 52 + 80
4Т = 132
Т = 132/4 = 33 °C
Ответ: 33.