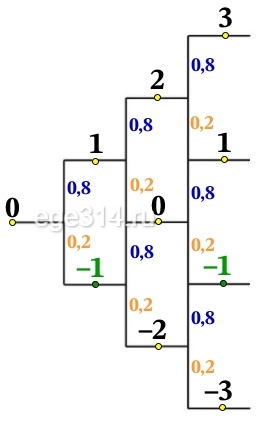
Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 0,8 на единицу больше предыдущего и с вероятностью 1 – р меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен –1?
Источник: mathege
Решение:
Задача о случайном блуждании.
Вероятность подняться вверх на 1, при каждом шаге равна p = 0,8.
Вероятность спустится вниз на 1, при каждом шаге равна 1 – p = 1– 0,8 = 0,2.
Начинаем движение с 0. Пусть P_{0\to -1} вероятность, когда либо попасть в –1, находясь сейчас в 0.
Мы можем сразу на первом шаге попасть в –1 ИЛИ пойти в 1 и от туда попасть каким либо путём в –1, вероятность этого равна:
P_{0\to -1}=0,2{\color{Blue}+}0,8\cdot P_{1\to -1}
Заметим, что спуски и подъёмы между соседними числами, везде происходят с равной вероятностью тогда:
P_{1\to -1}=P_{0\to -1}\cdot P_{0\to -1}
(нужно дважды проделать путь, равный расстоянию от 0 до –1)
Получаем обычное квадратное уравнение:
P_{0\to -1}=0,2+0,8\cdot (P_{0\to -1})^{2}\\ 0,8(P_{0\to -1})^{2}-P_{0\to -1}+0,2=0{\color{Blue} |\cdot 5}\\4(P_{0\to -1})^{2}-5P_{0\to -1}+1=0
D = (–5)2 – 4·4·1 = 25 – 16 = 9 = 32
P_{0\to -1}=\frac{5+3}{2\cdot 4}=1\\P_{0\to -1}=\frac{5-3}{2\cdot 4}=0,25
Т.к. исходная вероятность подняться вверх была больше (т.е. отдалится от –1), чем спустится вниз к –1, выбираем в ответ меньшую вероятность 0,25 (если было бы наоборот, то ответ был бы 1).
Ответ: 0,25.