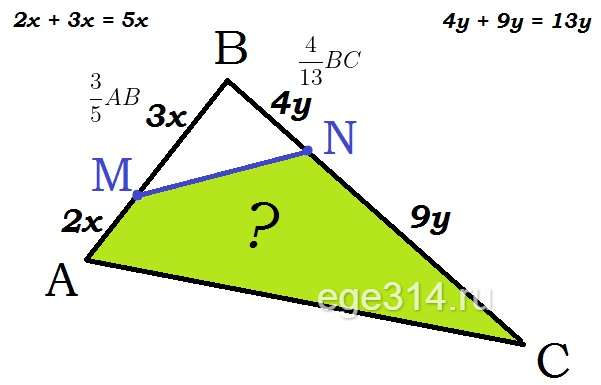
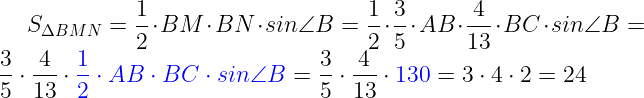На сторонах АВ и ВС треугольника АВС взяты соответственно точки M и N так, что AM:MB = 2:3 и BN:NC = 4:9. Найдите площадь четырехугольника AMNC, если площадь треугольника АВС равна 130.
Решение:
Площадь четырёхугольника AMNC равна:
SAMNC = SΔABC – SΔBMN = 130 – SΔBMN
Площадь треугольника АВС:
SΔABC = \color{Blue} \frac{1}{2}·AB·BC·sin ∠B = 130
Выразим стороны ΔBMN через стороны ΔABC:
BM=\frac{3}{5}AB\\BN=\frac{4}{13}BC
Найдём площадь треугольника BMN:
Найдём площадь четырёхугольника AMNC:
SAMNC = SΔABC – SΔBMN = 130 – 24 = 106
Ответ: 106.