Площадь основания кругового конуса равна 64π см2. Образующая конуса длиннее его высоты на 2 см. Найти отношение площади боковой поверхности конуса к площади его основания.
Решение:
Sосн = πr2 = 64π ⇒ r = 8
Образующая: l
Высота: l – 2
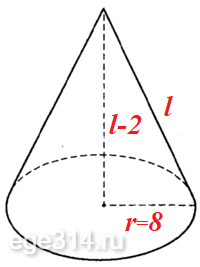
По теореме Пифагора найдём образующую l:
(l – 2)2 + 82 = l2
l2 – 4l + 4+ 64 = l2
–4l = –68
l = 17
Площадь боковой поверхности конуса равна:
Sбок = πrl = π·8·17 = 136
Отношение площади боковой поверхности конуса к площади его основания равно:
\frac{S_{бок}}{S_{осн}}=\frac{136\pi}{64\pi}=2,125
Ответ: 2,125.