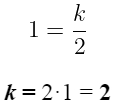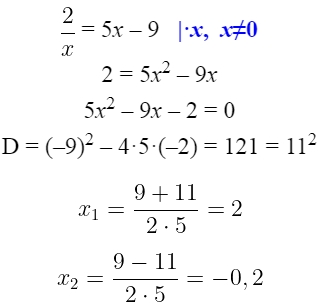На рисунке изображён график функции f(x) = \frac{k}{x} и g(x) = ax + b, которые пересекаются в точках А и В. Найдите абсциссу точки В.
Источник: mathege
Решение:
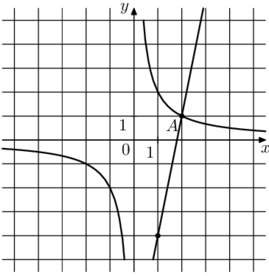
Подставим точку (2;1) найдём k гиперболы:
Гипербола имеет вид:
Найдём a и b прямой.
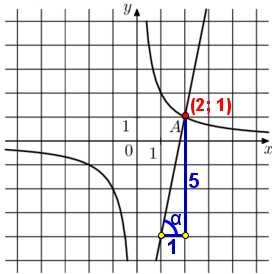
a – тангенс угла наклона прямой, по отношению к оси х. Тангенс это отношение противолежащего катета, к прилежащему катету:
Подставим точку (2; 1) найдём b прямой:
1 = 5·2 + b
b = 1 – 10 = –9
Функции прямой имеет вид:
y = 5x – 9
Найдём абсциссы точек пересечения функций:
У точки А координата х = 2, значит у точки В координата х = –0,2.
Ответ: –0,2.