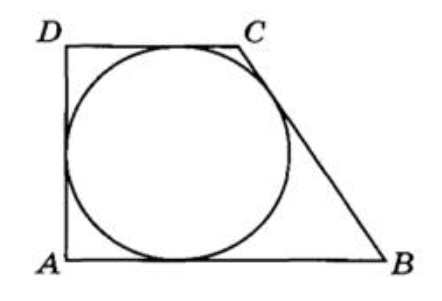
Периметр прямоугольной трапеции, описанной около окружности, равен 100, её большая боковая сторона равна 37. Найдите радиус окружности.
Источники: fipi, os.fipi, Досрочная волна 2015
Решение:
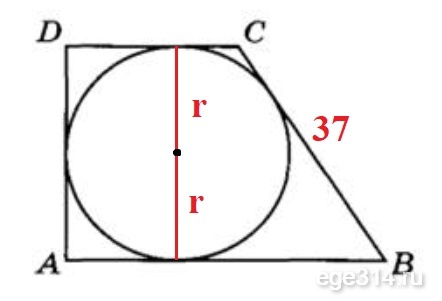
По свойству описанного около окружности четырёхугольника:
AD + CВ = DC +AB
По условию:
P = AD + CВ + DC + AB = 100
Найдём AD:
AD + CВ = \frac{100}{2} = 50
AD = 50 – CВ = 50 – 37 = 13
AD равен диаметру, тогда радиус равен:
r = \frac{AD}{2}=\frac{13}{2} = 6,5
Ответ: 6,5.