В треугольнике АВС известны длины сторон АВ = 12, АС = 72, точка О – центр окружности, описанной около треугольника АВС. Прямая ВD, перпендикулярная прямой АО, пересекает сторону АС в точке D. Найдите СD.
Источник: ОГЭ Ященко 2023 (36 вар)
Решение:
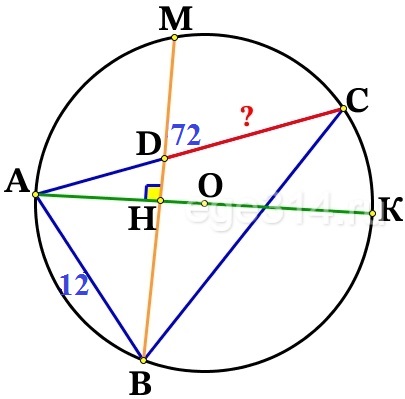
Диаметр АК⊥ хорде BM в точке Н, тогда BH = НМ.
Достроим ΔВАМ – он равнобедренный (АН – высота и медиана), значит углы при основании равны ∠АВМ = ∠АМВ.
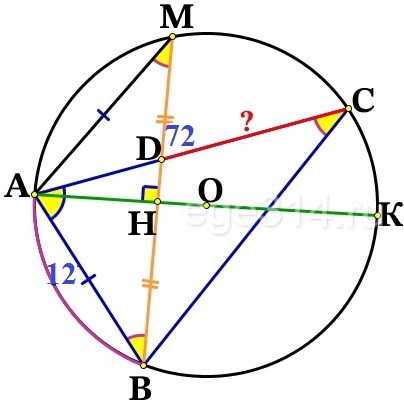
∠АМВ = ∠АСВ как вписанные, опирающиеся на одну и ту же дугу ‿АВ.
ΔADB подобен ΔАВС, по двум равным углам (∠А – общий, ∠АВD = ∠АСВ), значит соответствующие стороны треугольников пропорциональны, составим пропорцию:
\frac{AB}{AC}=\frac{AD}{AB}=\frac{BD}{BC}\\\frac{AB}{AC}=\frac{AD}{AB}\\\frac{12}{72}=\frac{AD}{12}\\AD=\frac{12\cdot 12}{72}=\frac{1\cdot 12}{6}=2
Найдём DC:
DC = AC – AD = 72 – 2 = 70
Ответ: 70.