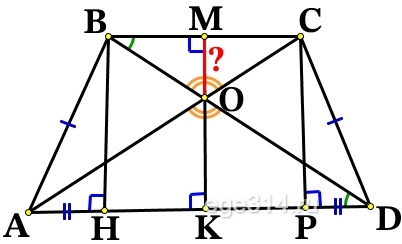
Решение №2408 В равнобедренную трапецию, периметр которой равен 20, а площадь равна 20, можно вписать окружность

Решение:

    Проведём высоты из вершин В, С и через точку пересечения диагоналей О (ВН = МК = СР). Искомое расстояние это МО:

    Трапеция равнобедренная, значит боковые стороны равны: 

AB = СD

    Если в трапецию можно вписать окружность, то сумма противоположных сторон равна:

ВС + AD = AB + CD = 2AB

    Периметр равен 160, сумма всех сторон трапеции:

ВС + AD + AB + CD =20
2AB + 2AB = 20
4AB = 20
AB = 20/4 = 5
CD = 5

    Площадь трапеции равна 20:

S=\frac{a+b}{2}\cdot h\\20=\frac{BC+AD}{2}\cdot MK\\20=\frac{2\cdot AB}{2}\cdot MK\\20=\frac{2\cdot 5}{2}\cdot MK\\20=5\cdot MK\\MK=\frac{20}{5}=4
МК = ВН = СР = 4

    В прямоугольном ΔАВH найдём АН по теореме Пифагора:

AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{5^{2}-4^{2}}=\sqrt{9}=3

    АН = РD = 3 – как отрезки образованные высотами равнобедренной трапеции.

ВС + AD = 2·AB
ВС + HP + AH + PD = 2·5
2ВС + 2·3 = 10
2ВС = 10 – 6
2ВС = 4
ВС = 4/2 = 2

    Найдём AD:

AD = AH + HP + PD = BC + 2·AH = 2 + 2·3 = 8

    Пусть искомое расстояние МО = х, тогда ОК = МК – МО = 4 – х.
    ΔВОС подобен ΔАОD по двум равным углам, ∠ВОС = ∠АОD как вертикальные, ∠СВО = ∠АDО – как накрест лежащие при двух параллельных прямых и секущей. 
    Значит в данных треугольника соответствующие стороны и высоты пропорциональны, составим отношение:

\frac{BC}{AD}=\frac{MO}{OK}\\\frac{2}{8}=\frac{x}{4-x}\\\frac{1}{4}=\frac{x}{4-x}
4x = 1·(4 – x)
4x = 4 – x
4x + x = 4
5x = 4
x = 4/5 = 0,8

Ответ: 0,8.